For the last few years I’ve been dabbling with data in football, especially with data visuals that show performance or intention. For the most part I have only focused on that was familiar within the data and focused on representation of data and the manipulation of it. But since I’ve worked more and more with data in big datasets, I’ve also realised that differences in outcome also have a lot to do with the methodology you are using.
In this article I will focus on specific data metric and which score we can give each player. But, to do that I will also compare two forms of deviations to calculate a z-score: the Standard Deviation and the Mean Absolute Deviation.
Contents
- Data
- Shot-stopping explainer
- Moving away from percentile ranks
- Standard Deviation (SD)
- Mean Absolute Deviation (MAD)
- Z-scores
- Best shot-stopper profiles
- Final thoughts
- Data
The data I’m using in this article comes from Opta. This Opta data has been released on the website of FBRef. The specific data was downloaded on March 21st, 2024.
The data metric I’m using is the PsxG +/-. This metric is the saldo of Post-shot expected goals minus the goals conceded. This metric shows us whether a goalkeeper saves more or fewer shots than is expected based on the probability of the shots going in.
Obviously only goalkeepers are included because we are looking at a goalkeeper specific metric, but some other filters do apply. I’m only looking at the goalkeepers playing in the tradition top-5 leagues in Europe, which are the English Premier League, Spanish La Liga, French Ligue 1, German Bundesliga and the Italian Serie A. There are only goalkeepers included that have 500 minutes played — this is done for representative data.
What is shot-stopping and how do we measure it?
Shot-stopping is one of the essential parts of the goalkeeper’s game and it focuses on stopping balls going into goal from shot. It’s basically how well a keeper responds to shots from the attacking side and also coincides with the more conservative approach of a goalkeeper’s duty: stopping shots.
Of course, we can look at shots faced and how many saves are made, but that doesn’t only say something about the goalkeeper — but also about the defence, so we have a need to measure the quality of a shot and therefore also the probability of the shot going into the goal.
Different data providers have created metrics for it. Wyscout has prevented goals, Statsbomb has GSAA (goals saved above average) and Opta — the metric we are focusing one — has PsxG +/-. With the latest one we are looking at post-shot expected goals — the probability after the shot is done — minus the actual goals conceded. This gives us an idea whether a goalkeeper is better than the expected goals would suggest.
Moving away from percentile ranks

To compare goalkeepers to each other there are several things we can do in terms of data. Percentile ranks are used in data analysis for several reasons. Firstly, percentile ranks provide a standardised way to compare individual data points within a larger dataset. By converting raw data into percentiles, we can understand the relative position or performance of a specific data point compared to the rest of the data in our files.
Additionally, percentile ranks allow for easier interpretation and communication of data. Instead of dealing with raw values, which can vary widely depending on the scale or unit of measurement, percentile ranks provide a common language to discuss and compare data points. For example, saying that a player’s performance is in the 90th percentile indicates that they outperformed 90% of the other players in the dataset.
Percentile ranks help mitigate the impact of outliers or extreme values. By focusing on the position of a data point within the distribution, extreme values have less influence on the overall analysis. This can be particularly important in cases where outliers can skew the interpretation of data.
So, why move away from this?
When we take the 50th percentile that will mean the middle value within a dataset. When we look at z-scores, we focus on the 50th (when converted from 0–100) as the most common value — which does help with making sure that outliers don’t have as big of an influence on the calculation.
We are going to look at two different deviations to show who is doing very well in terms of PsxG +/-
Standard Deviation (SD)
Standard deviation is calculated by taking the square root of a value derived from comparing data points to a collective mean of a dataset. The formula is:

In terms of football, we are going to calculate the mean from the whole dataset with the mean being the most common value of the data metric of PsxG +/-. And with differences from the mean, we are calculating the deviations.

So with doing that we can see in a more concise manner how a player comes close to the mean or deviates from it. So by using z-scores with standard deviation it provides a more precise measure of relative position within a distribution compared to percentile ranks. A z-score of 1.5, for instance, indicates that a data point is 1.5 standard deviations above the mean, allowing for a more granular understanding of its position.
Mean Absolute Deviation
The mean absolute deviation (MAD) is a measure of variability that indicates the average distance between observations and their mean. MAD uses the original units of the data, which simplifies interpretation. Larger values signify that the data points spread out further from the average. Conversely, lower values correspond to data points bunching closer to it. The mean absolute deviation is also known as the mean deviation and average absolute deviation.

This definition of the mean absolute deviation sounds similar to the standard deviation (SD). While both measure variability, they have different calculations. In recent years, some proponents of MAD have suggested that it replace the SD as the primary measure because it is a simpler concept that better fits real life.
Why we can use this form of deviation is that you use absolute values and that there is a closer variable that incorporates outliers better than the standard deviation.
Z-scores
One of the key benefits of z-scores is that they allow for the standardization of data by transforming it into a common scale. This is particularly useful when dealing with variables that have different units of measurement or varying distributions.
By calculating the z-score of a data point, we can determine how many standard deviations it is away from the mean of the distribution. This standardized value provides a meaningful measure of how extreme or unusual a particular data point is within the context of the dataset.
Z-scores are also helpful in identifying outliers. Data points with z-scores that fall beyond a certain threshold, typically considered as 2 or 3 standard deviations from the mean, can be flagged as potential outliers. This allows analysts to identify and investigate observations that deviate significantly from the rest of the data, which may be due to measurement errors, data entry mistakes, or other factors.
With Z-Scores, we calculate the score 50, differently from the 50th percentile. While percentiles look at the middle value or median, Z-scores look at the average or mean of the dataset.
Best shot-stopper profiles
Now we have looked at the two different methods of calculating z-scores, we will have to look closer at what it means for the scores when looking at goalkeepers.
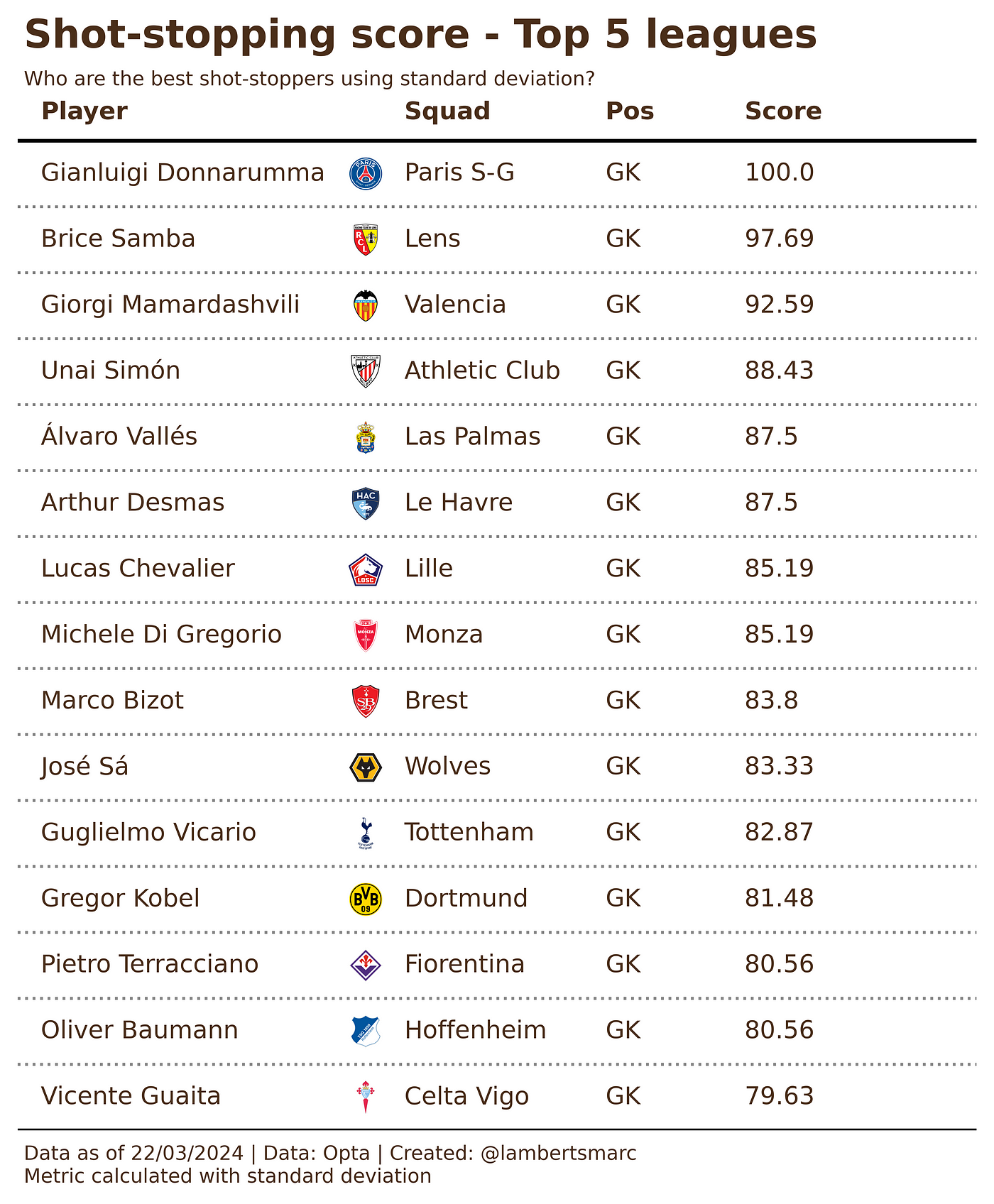
Using the z-scores with standard deviation, we see the following goalkeepers as being the best shot-stoppers:
Using the z-scores with mean absolute deviation, we see the following goalkeepers as being the best shot-stoppers:

We have calculated the scores for PsxG +/- with both methods using deviations and the scores are exactly the same when we convert z-scores to 0–100. This is both to be expected and not — mostly because there are no big outliers, so we won’t see a difference in the scores.
If we look at the deviations away from, perhaps we can see something different. The standard deviation:

If we look at the deviations away from, perhaps we can see something different. The mean absolute deviation:

When we look at the deviations away from the mean, we can definitely see that there is a difference in the standard deviations and the mean absolute deviations. In general we can tell that the deviations from the mean are bigger when using mean absolute deviations. This also because they are a bit compliant with validating outliers in the data.
Final thoughts
Using both standard deviations and mean absolute deviations (MAD) in data analysis offers complementary insights into the variability or dispersion of a dataset.
Standard deviation (SD) is a measure that reflects the average distance of data points from the mean. It is widely used in statistical analysis and is commonly interpreted within the context of the normal distribution. However, SD is sensitive to outliers because it squares the deviations from the mean, giving more weight to larger deviations.
On the other hand, mean absolute deviation (MAD) measures the average absolute distance of data points from the mean. It is less sensitive to outliers because it does not square deviations, thus giving extreme values less influence on the measure. MAD provides a more robust measure of dispersion, particularly in datasets with outliers or non-normally distributed data.
The main takeaway from using both SD and MAD lies in their complementarity. While SD is more commonly used and easier to interpret, MAD offers a clearer picture of the spread of data in certain situations, especially when dealing with outliers or non-normally distributed data. By using both measures together, analysts can gain a more comprehensive understanding of the variability present in the dataset, allowing for more informed decisions and interpretations in various fields of analysis such as finance, economics, and science.

Geef een reactie